1. Introduce a point particle having single degree of freedom.
The system's Lagrangian is described as
\[
L = L(q, \dot{q}, t).
\]
Assume the point particle started moving at P_1 when time is \(t=t_1\)
and arrived at P_2 when time is \(t=t_2\).
Let us introduce the action integral:\(S\) defined as
\[
S = \int^{t_2}_{t_1} L dt.
\]
According to principle of least action, the motion of the point particle is
constrained so that the value of S to be minimum.
This implies that when the motion is to be a bit off from the proper path
\((q+\delta q, \dot{q}+\delta{\dot{q}})\), the action integral does not change
against
any kind of \(\delta q \text{ and } \delta \dot{q} \).
Thus,
\[
\delta S = \delta \int^{t_2}_{t_1} L dt = 0.
\]
Based on the relation above, derive Euler•Lagrange equation;
\[
\frac{\partial L}{\partial q} - \frac{d}{dt} \left( \frac{\partial L}{\partial
\dot{q}} \right). \tag{2.1}
\]
Note that the \(P_1\):start and \(P_2\):end are fixed
and \(\delta(t_1) = \delta{t_2} = 0\). Furthermore,
\(\delta q \text{ and } \delta \dot{q}\) is so small that you may ignore
all terms higher than the second order.
solution
\[
\delta L = \frac{\partial{L}}{\partial{q}} \delta q + \frac{\partial L}{\partial
\dot{q}}
\delta \dot{q}
\]
Use integration by parts,
\[
\int \frac{\partial L}{\partial \dot{q}} \delta \dot{q} dt
= - \int \frac{d}{dt} \Big( \frac{\partial L}{\partial \dot{q}} \Big) \delta q
dt
+ \left[ \frac{\partial L}{\partial \dot{q}} \delta q dt \right]
\]
Then,
\[
\delta S = \int^{t_2}_{t_1} \delta L dt
\]
\[
= \int^{t_2}_{t_1} \frac{\partial L}{\partial q} \delta q + \frac{\partial
L}{\partial \dot{q}} \delta \dot{q} dt
\]
\[
= \left[ \frac{\partial L}{\partial \dot{q}} \delta q \right]^{t_2}_{t_1}
+ \int^{t_2}_{t_1} \left\{ \frac{\partial L}{\partial q}
- \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}} \right) \right\} \delta
q =
0
\]
Thus,
\[
\frac{\partial L}{\partial q}
- \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}} \right)
= 0
\]
2. Assume a system that the Lagrangian is constant against translation of the
coordinate \(q \rightarrow q + \Delta q \). In that context, \(p\) conserves.
\[
p \equiv \frac{\partial L}{\partial \dot{q}}
\]
This can be understood from Euler•Lagrange equation;
the first term of the equation is to be 0. This is also corresponds to the
law of the conservation of momentum.
Meanwhile, when the Lagrangian is constant against translation of time \(t
\rightarrow t + \Delta t\),
show the energy conservation described as following equation. Hint; solve
total differential of L.
solution
The answer should satisfy \(dE = 0\).
\[
dE = d (p\dot{q} - L)
\]
\[
= d(p\dot{q}) - dL \tag{2.2.1}
\]
Also,
\[
dL = \frac{\partial L}{\partial q} dq + \frac{\partial{L}}{\partial \dot{q}}
d\dot{q} + \frac{\partial L}{\partial t} dt \tag{2.2.2}
\]
Here,
\[
\frac{\partial L}{\partial t} dt = 0, \, \frac{\partial L}{\partial \dot{q}} =
p, \,
\frac{\partial L}{\partial q} = \frac{d}{dt} \left( \frac{\partial L}{\partial
\dot{q}} \right)
\]
Thus, rearrange the equation \((2.2.2)\),
\[
dL = \frac{\partial L}{\partial q} dq + \frac{\partial L}{\partial \dot{q}}
d\dot{q}.
\]
\[
dL = \dot{p} dq + p d\dot{q} = d(p\dot{q}) \tag{2.2.3}
\]
Substitute \((2.2.3)\) for \((2.2.1)\),
\[
dE = d(p\dot{q}) - d(p\dot{q}) = 0
\]
3. As shown in Fig. 2.1, at the cylindrical coordinate system,
the point particle having mass of \(m\) moves smoothly along with the wire
which is fixed to \(z = f(r)\). \(f(0) = 0\), the wire is continuous and
\(f(r)\) can be differentiable.
(1) Describe this system's Lagrangian \(L\) using \(m, g, \omega, r, \dot{r}, f,
f'(=\frac{df}{dr})\). Note that the Lagrangian is \(L = K - U\), where \(K\) is
the kinematic energy and \(U\) is the potential energy.
solution
The location of the point particle in orthogonal coordinate system is,
\[
(x, y, z) = (r\cos{\omega t}, r\sin{\omega t}, f(r)).
\tag{2.3.1}
\]
Differentiate Eq. (2.3.1) by \(t\).
\[
(\dot{x}, \dot{y}, \dot{z}) = (\dot{r}\cos{\omega t} - r\omega\sin{\omega t},
\dot{r}\sin{\omega t} + r\omega \cos{\omega t}, \dot{r}f')
\]
Thus,
\[
v^2 = \dot{x}^2 + \dot{y}^2 + \dot{z}^2
\]
\[
= \dot{r}^2\cos^2{\omega t} - 2\dot{r}r\omega\cos{\omega t}\sin{\omega t} +
r^2\omega^2\sin^2{\omega t}
\]
\[
+ \dot{r}^2\sin^2{\omega t} + 2\dot{r}r\omega\cos{\omega
t}\sin{\omega t} + r^2\omega^2\cos^2{\omega t}
\]
\[
+ \dot{r}f^{'2}
\]
\[
= \dot{r} + r^2\omega^2 + \dot{r}f^{'2}
\]
\[
L = T - U = \frac{1}{2} m (\dot{r}^2 + r^2\omega^2 + \dot{r}f^{'2}) - mgf(r)
\tag{2.3.2}
\]
(2) When the point particle remain stationary (\(\dot{r} = 0\)),
substitute L for Eq. \((2.1)\), then describe \(f(r)\) using \(g, \omega, r\).
solution
Substitute \(L\) of Eq.\((2.3.2)\) for \(L\) in Eq.\((2.1)\)
\[
\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{r}} \right)
= m\ddot{r} + m\ddot{r}f^{'2} + 2m\dot{r}^2 \frac{df(r)}{dt}\frac{d^2f(r)}{dr^2}
\]
When \(\dot{r} = \ddot{r} = 0\),
\[
\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{r}} \right) = 0
\]
\[
\frac{\partial L}{\partial r} = mr\omega^2 - mgf(r)'
\]
\[
0 = r\omega^2 - g f(r)'
\]
\[
f(r)' = \frac{\omega^2}{g} r
\]
\[
\frac{df(r)}{dr} = \frac{\omega^2}{g}r
\]
\[
f(r) = \frac{\omega^2}{2g} r^2 + C
\]
From the initial condition, the constant \(C\) is
\[
f(0) = 0, C = 0
\]
Finally,
\[
f(r) = \frac{\omega^2}{2g} r^2
\]
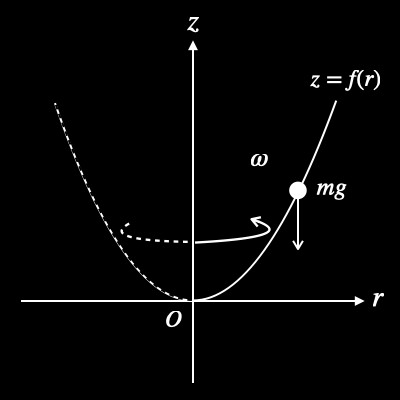 Fig. 2.3.1
Fig. 2.3.1